DANIEL BERNOULLI  1700 - 1782  (W3, AN, G1, G2, G3a)

Acknowledgements

Bernoulli: detail, by the German artist Johann Niklaus Grooth (1723-1797), 1790 – location unknown. Diagram: licensed under Creative Commons – https://en.wikipedia.org/wiki/Bernouilli’s_princiiple. Euler: by the Swiss painter Jacob Emmanuel Handmann (1718-1781), 1753 – Kunstmuseum, Basel, Switzerland.

G2-1727-1760-G2-1727-1760-G2-1727-1760-G2-1727-1760-G2-1727-1760-G2-1727-1760-G2

xxxxxThe brilliant Swiss mathematician and physicist Daniel Bernoulli was born in Groningen in the Netherlands, the son of Johann Bernoulli and the nephew of Jacques Bernoulli, both outstanding mathematicians of their day. After studying philosophy and medicine at the universities of Heidelberg, Strasbourg and Basel, he was appointed professor of mathematics at the Russian Academy of Sciences in St. Petersburg at the age of twenty-five. It was here that he collaborated with his fellow mathematician and countryman Leonhard Euler until 1733, when he left St. Petersburg to take the chair of anatomy and botany at Basel University. He later lectured in physiology and physics.

xxxxxThroughout a long career he made notable advances in the study of trigonometry and differential equations. In 1724, for example, he produced his Exercitationes quaedam Mathematicae - the work which gained him his post at St. Petersburg - but his reputation today rests mainly on his contribution in the field of hydrodynamics, set out in his major work Hydrodynamica and published in 1738. This was a practical as well as a theoretical study of the pressure and velocity of fluids, and it contained what has come to be known as Bernoulli's principle or theorem. Arrived at by the application of Isaac Newton's laws of motion, this states that the pressure of a moving liquid or gas decreases the faster it flows, a principle which, in practice, can be applied to measure, for example, the movement of a ship's propeller, the upward force that lifts an aircraft's wings, or even the turn of a spinning ball in flight. 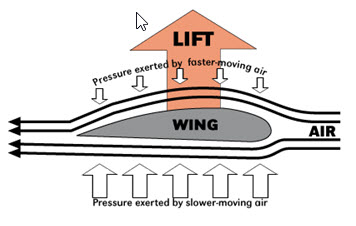In this work he also took the first steps towards developing the kinetic theory of gases, attempting a mathematical explanation of their behaviour based on the assumption that gases were made up of a vast number of particles or molecules.

xxxxxA highly inquisitive man who was ever striving to broaden and popularise scientific knowledge, he also produced papers on a wide variety of other subjects, including astronomy, magnetism, marine technology and oceanography. For such work he won no less than ten prizes from the Paris Academy of Sciences.

xxxxxThe Swiss mathematician Leonhard Euler (1707-83), who collaborated with Daniel Bernoulli when they both worked at St. Petersburg, made an outstanding contribution to the founding of pure mathematics. He was born in Basel, and studied at the city's university, where he was a pupil of Bernoulli's father, Johann, and obtained his master's degree at the age of sixteen. In 1727 he was invited to Russia by Empress Catherine I to work at the Academy of Sciences in St. Petersburg. He was appointed professor of physics there in 1730, and then of mathematics three years later when Daniel Bernoulli left to go back to Basel. In 1741, at the insistence of Frederick the Great, he went to Berlin and was professor of mathematics at the Academy of Sciences there for twenty-five years, not returning to St. Petersburg until 1766.

xxxxxDuring his first stay in St. Petersburg in the 1720s he began to lose his sight, and towards the end of his life he was almost totally blind. This obviously slowed down his work rate, but despite this disability, he wrote several major works and, in addition, produced hundreds of mathematical and scientific papers. These books and papers introduced many new concepts and a variety of techniques with which to solve problems. He was responsible, for example, for the introduction of many current notations, such as the method of naming the sides and angles of a triangle, and the use of the symbol pi for working out the circumference of a circle.

xxxxxHis Introduction to the Analysis of Infinities, published in 1748, together with other works, marks him out as one of the greatest mathematicians of the 18th century. In it, Euler not only gave a masterly summary of known data, but he also gave the first strictly analytical treatment of algebra, the theory of equations, trigonometry and analytical geometry. Nor were other branches neglected. In the theory of numbers it is to Euler that we owe the discovery, in 1783, of the law of quadratic reciprocity, a vital part of the modern theory. Furthermore, his Institution of Differential and Integral Calculus, produced in separate volumes, and his Introduction to Algebra, published in 1770, provided a comprehensive coverage of these subjects and, as such, proved first-class textbooks. And in practical terms, Euler was successful in using calculus to solve physical as well as mathematical problems.

xxxxxBut, like Bernoulli, Euler's interests were not confined to one scientific discipline. He also put his mind to a variety of subjects, including astronomy, mechanics, optics and acoustics. The basic principles of a number of these subjects were contained in his Lettres à une princess d'Allemagne, begun in 1768 and written over four years. In astronomy, he attempted to make a more precise calculation of the moon's movements, and he made some headway despite the problems associated with the interactions of moon, sun and earth. This led to work on the fluctuation of tides and an interest in fluid mechanics, Bernoulli's particular line of research, but to which Euler contributed.